2021牛客寒假算法基础集训营1-E-三棱锥之刻

题面

https://ac.nowcoder.com/acm/contest/9981/E

读题

很显然, 这是一道计算几何题, 我们可以运用高中知识求解.

现在我们来分类讨论, 很显然有以下情况: + r小于等于正三棱锥的内切球半径时, s等0 + r大于等于正三棱锥的外接球半径时, s等于正三棱锥的表面积 > 当r介于二者之间时, 我们设球体被三棱锥的一个面所截得到的圆为O, 又有两种情况: > + O内含于三角形中, 此时根据几何知识求得O的半径再计算面积即可 > + O相交于三角形, 此时要求的面积就是O的面积减去三个弓形的面积, 下面做公式推导

公式推导

首先给出公式:

我们可以利用弓形面积公式来推导 弓形面积公式: 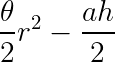其中θ为圆心角, r为半径, a为弦长, h为圆心与弦构成的三角形的高

具体推导过程略

完整AC代码

点我查看完整代码

#include<bits/stdc++.h>
using namespace std;
const double pi = acos(-1);
double a, r;
int main(){
    scanf("%lf%lf", &a, &r);
    if (r >= (sqrt(6) * a) / 4){
        printf("%.7lf", sqrt(3) * a * a);
    }
    else if (r <= (sqrt(6) * a) / 12){
        printf("%.7lf", 0.0);
    }
    else if (r * r <= a * a / 8){
        double t = (r * r) - a * a / 24.0;
        double ans = 4 * pi * t;
        printf("%.7lf", ans);
    }
    else{
        double t = (r * r) - a * a / 24.0;
        double s = sqrt(3) * a;
        double u = sqrt(r * r - a * a / 8);
        double s1 = pi * t;
        double s2 = atan(u * 6 / s) * t - u * s / 6;
        double ans = 4 * (s1 - 3 * s2);
        printf("%.7lf", ans);
    }
    return 0;
}